Derive zero coupon yield curve
Contents:
- pinky girl coupons.
- Construct and analyze zero curves.
- cap coupon code.
Also, two identical coupons belonging to two bonds with different maturities will not be discounted at the same yield, whereas they generate the exact same cash flow. To overcome these problems, one constructs a zero-coupon yield curve from the prices of these traded instruments. As a reminder, the zero-coupon rate is the yield of an instrument that does not generate any cash flows between its date of issuance and its date of maturity. The technique used to achieve this is called bootstrapping, a term which describes a self-contained process that is supposed to proceed without external input.
This method is based on the assumption that the theoretical price of a bond is equal to the sum of the cash flows discounted at the zero-coupon rate of each flow. To illustrate this, let's take the example of a bond with a remaining lifetime of five years and an annual coupon of 3. Using a series of zero-coupon rates, the determination of which we will see later, we can determine the theoretical price of the bond:.
- lowes topsoil coupon?
- hollywood tan co coupons?
- Your Answer!
- widows walk coupon.
Based on this concept, we can build a zero-coupon curve starting from a set of bonds with different maturities. For the construction of our zero-coupon curve, we will take for example the following list of securities as a starting point:.
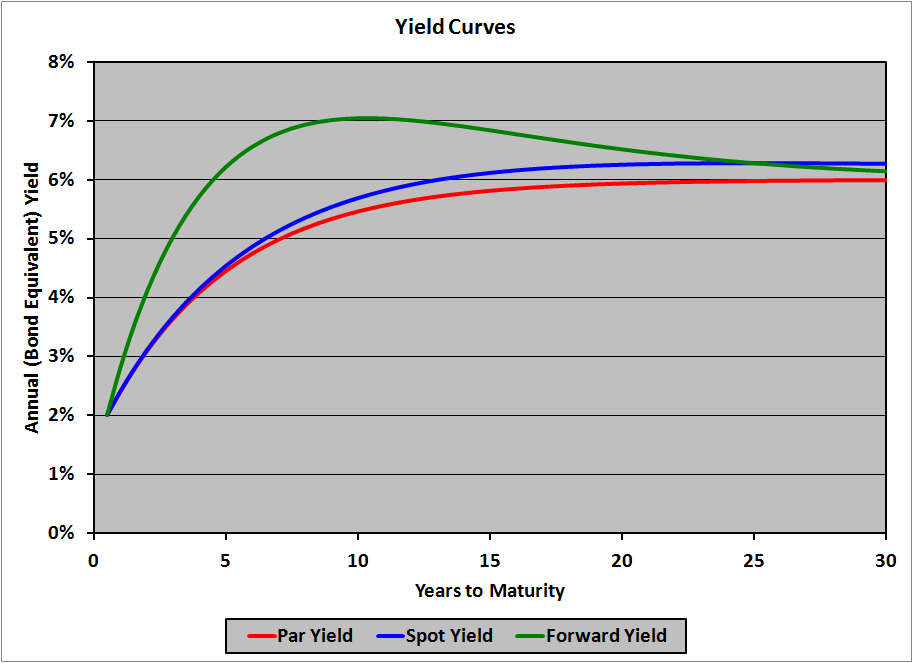
Bootstrapping the Zero Curve and Forward Rates
The first securities A, B and C actually are already zero coupons, since they generate no cash flows before maturity. This is generally the case for money market securities with a maturity of less than, or equal to, one year which remunerate their holders not through a coupon but through the difference between the issue price, which is below par, and the price at which they will be redeemed.
The preceding three yields have been calculated using this formula. We can then successively carry out the deduction of zero-coupon rates for the 2 and 3 year maturities. Already knowing the rate for one year maturity 2. To calculate the zero-coupon rate for the 2-year maturity, we will strip security D into two zero-coupons: Discounting the coupon of the first year of security D 3.
And we now have all the information required in order to calculate the zero-coupon rate as illustrated in the table below:. In order to obtain the 2-year zero-coupon rate, we just have to calculate, by iteration, the rate at which an amount of Having obtained the zero-coupon rates for the maturities 1 year 2. The 3-year zero-coupon rate we are looking for is therefore the one that verifies the following equation:.
The rate obtained, again by iteration, is 3.
The short answer to the original question is: Swaps are quoted at par, i. Its level therefore contains information about the quoter's estimates of Libor; if they think it will be higher, they would need a higher fix rate to balance the values of the legs.

William's answer is more direct. Swap rates can be used to calibrate a discount curve as follows, the full algebra follows this webpage: Bootstrapping the Discount Curve from Swap Rates.
Post navigation
This is the first point on the calibrated curve. We can continue this process for the next year's swap rate. A more general expression is given in the page I linked above.
By clicking "Post Your Answer", you acknowledge that you have read our updated terms of service , privacy policy and cookie policy , and that your continued use of the website is subject to these policies. Home Questions Tags Users Unanswered.
LIBOR; 1 year to 7 years: Interest Rate Swap; 7 years above: I'm a bit lost here: While interest rate swap is a contract among to legs. I was told that we need to build the swap curve before we try to value floating leg of an IRS.
Chapter 4 Deriving the Zero-Coupon Yield Curve FIXED-INCOME SECURITIES.
Then use the rates from each tenor in Swap curve to value the cashflows of IRS floating leg. And hint me if I am "believing" wrong concept. Market wise, above may be no longer in practice but improvised versions. Do you mean a bond representing the fixed leg of the swap?
Bootstrapping the Zero Curve and Forward Rates -
Hence the par rate of the bond is the same as the par swap rate. The methodology in this answer is unfortunately quite outdated. Theses discount curves can be represented in terms of yields r T: I am the author of the source code referenced and the paper. Christian Fries Christian Fries 1, 10 Phil H Phil H 2, 10 And fundig curve refers to your own swap curve?
Can you please share what are we using to build each libor and funding curve in your point?